Euler's totient function

For other functions named after Euler, see List of topics named after Leonhard Euler.

In number theory, Euler's totient or phi function, 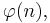$\varphi(n),$ is a arithmetical function that counts the number of positive integers less than or equal to n that are relatively prime to n. That is, if n is a positive integer, then φ(n) is the number of integers k in the range 1 ≤ k ≤ n for which gcd(n, k) = 1. The totient function is a multiplicative function, meaning that whenever two numbers m and n are relatively prime to each other then φ(mn) = φ(m)φ(n).

For example let n = 9. gcd(3, 9) = gcd(6, 9) = 3, and gcd(9, 9) = 9. The other six numbers 1, 2, 4, 5, 7 and 8 are coprime to 9. Therefore, φ(9) = 6. As another example, φ(1) = 1 since gcd(1, 1) = 1.

The totient function is important mainly because it gives the order of the multiplicative group of integers modulo n (the group of units of the ring 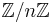$\mathbb{Z}/n\mathbb{Z}$ ). See Euler's theorem.
The totient function also plays a key role in the definition of the RSA encryption system.

History, terminology, and notation

Leonhard Euler introduced the function in 1760.^[1]^[2] The standard notation^[3]^[4] 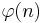$\varphi(n)$ is from Gauss's 1801 treatise Disquisitiones Arithmeticae.^[5] Thus it is usually called Euler's phi function or simply the phi function.

In 1883 J. J. Sylvester coined the term totient for this function,^[6] so it is also referred to as the totient function, the Euler totient, or Euler's totient. Jordan's totient is a generalization of Euler's.

The cototient of n is defined as 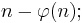$n - \varphi(n);$ i.e. the number of positive integers less than or equal to n that are divisible by at least one prime that also divides n.

Computing Euler's function

There are several formulae for the totient.

Euler's product formula

It states

$\varphi(n) =n \prod_{p\mid n} \left(1-\frac{1}{p}\right),$

where the product is over the distinct prime numbers dividing n. (The notation is described in the article Arithmetical function.)

The proof of Euler's product formula depends on two important facts.

φ(n) is multiplicative

This means that if gcd(m, n) = 1 then 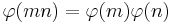$\varphi(mn) = \varphi(m) \varphi(n)$ .
(Sketch of proof: let A, B, C be the sets of residue classes modulo-and-coprime-to m, n, mn respectively; then there is a bijection between A × B and C, by the Chinese remainder theorem.)

φ(p^k) = p^k − p^{k − 1} = p^{k − 1}(p − 1)

That is, if p is prime and k ≥ 1 then

$\varphi(p^k) = p^k -p^{k-1} =p^{k-1}(p-1) = p^k \left( 1 - \frac{1}{p} \right).$

Proof: Since p is a prime number the only possible values of gcd(p^k, m) are 1, p, p², ..., p^k, and the only way for gcd(p^k, m) to not equal 1 is for m to be a multiple of p. The multiples of p that are less than or equal to p^k are p, 2p, 3p, ..., p^{k − 1}p = p^k, and there are p^{k − 1} of them. Therefore the other p^k − p^{k − 1} numbers are all relatively prime to p^k.

Proof of the formula: The fundamental theorem of arithmetic states that if n > 1 there is a unique expression for n,

$n = p_1^{k_1} \cdots p_r^{k_r},$

where p₁ < p₂ < ... < p_r are prime numbers and each k_i ≥ 1. (The case n = 1 is corresponds to the empty product.)

Repeatedly using the multiplicative property of φ and the formula for φ(p^k) gives

$\begin{align} \varphi(n) &= \varphi(p_1^{k_1}) \varphi(p_2^{k_2}) \cdots\varphi(p_r^{k_r})\\ &= p_1^{k_1} \left(1- \frac{1}{p_1} \right) p_2^{k_2} \left(1- \frac{1}{p_2} \right) \cdots p_r^{k_r} \left(1- \frac{1}{p_r} \right)\\ &= p_1^{k_1} p_2^{k_2} \cdots p_r^{k_r} \left(1- \frac{1}{p_1} \right) \left(1- \frac{1}{p_2} \right) \cdots \left(1- \frac{1}{p_r} \right)\\ &=n \left(1- \frac{1}{p_1} \right)\left(1- \frac{1}{p_2} \right) \cdots\left(1- \frac{1}{p_r} \right). \end{align}$

This is Euler's product formula.

Example

$\varphi(36)=\varphi\left(2^2 3^2\right)=36\left(1-\frac{1}{2}\right)\left(1-\frac{1}{3}\right)=36\cdot\frac{1}{2}\cdot\frac{2}{3}=12.$

In words, this says that the distinct prime factors of 36 are 2 and 3; half of the thirty-six integers from 1 to 36 are divisible by 2, leaving eighteen; a third of those are divisible by 3, leaving twelve coprime to 36. And indeed there are twelve: 1, 5, 7, 11, 13, 17, 19, 23, 25, 29, 31, and 35.

Fourier transform

The totient is the discrete Fourier transform of the gcd: (Schramm (2008))

$\varphi (n)=\sum\limits_{k=1}^n \gcd(k,n) e^{{-2\pi i}\tfrac{k}{n}}.$

The real part of this formula is

$\varphi (n)=\sum\limits_{k=1}^n \gcd(k,n) \cos {2\pi\frac{k}{n}}.$

Note that unlike the other two formulae (the Euler product and the divisor sum) this one does not require knowing the factors of n.

Divisor sum

Euler's classical formula^[7]^[8]

$\sum_{d\mid n}\varphi(d)=n,$

where the sum is over all positive divisors d of n, can be proven in several ways. (see Arithmetical function for notational conventions.)

One way is to note that 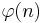$\varphi(n)$ is also equal to the number of possible generators of the cyclic group C_n. Since every element of C_n generates a cyclic subgroup and the subgroups of C_n are of the form C_d where d | n, the formula follows. ^[9] In the article Root of unity Euler's formula is derived by using this argument in the special case of the multiplicative group of the nth roots of unity.

This formula can also be derived in a more concrete manner.^[10] Let n = 20 and consider the fractions between 0 and 1 with denominator 20:

$\tfrac{ 1}{20},\,\tfrac{ 2}{20},\,\tfrac{ 3}{20},\,\tfrac{ 4}{20},\, \tfrac{ 5}{20},\,\tfrac{ 6}{20},\,\tfrac{ 7}{20},\,\tfrac{ 8}{20},\, \tfrac{ 9}{20},\,\tfrac{10}{20},\,\tfrac{11}{20},\,\tfrac{12}{20},\, \tfrac{13}{20},\,\tfrac{14}{20},\,\tfrac{15}{20},\,\tfrac{16}{20},\, \tfrac{17}{20},\,\tfrac{18}{20},\,\tfrac{19}{20},\,\tfrac{20}{20}$

Put them into lowest terms:

$\tfrac{ 1}{20},\,\tfrac{ 1}{10},\,\tfrac{ 3}{20},\,\tfrac{ 1}{ 5},\, \tfrac{ 1}{ 4},\,\tfrac{ 3}{10},\,\tfrac{ 7}{20},\,\tfrac{ 2}{ 5},\, \tfrac{ 9}{20},\,\tfrac{ 1}{ 2},\,\tfrac{11}{20},\,\tfrac{ 3}{ 5},\, \tfrac{13}{20},\,\tfrac{ 7}{10},\,\tfrac{ 3}{ 4},\,\tfrac{ 4}{ 5},\, \tfrac{17}{20},\,\tfrac{ 9}{10},\,\tfrac{19}{20},\,\tfrac{ 1}{ 1}$

First note that all the divisors of 20 are denominators. And second, note that there are 20 fractions.
Which fractions have 20 as denominator? The ones whose numerators are relatively prime to 20 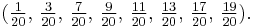$(\tfrac{ 1}{20},\,\tfrac{ 3}{20},\,\tfrac{ 7}{20},\,\tfrac{ 9}{20},\,\tfrac{ 11}{20},\,\tfrac{13}{20},\,\tfrac{17}{20},\,\tfrac{19}{20}).$
By definition this is φ(20) fractions.
Similarly, there are φ(10) = 4 fractions with denominator 10 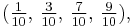$(\tfrac{ 1}{10},\,\tfrac{ 3}{10},\,\tfrac{ 7}{10},\,\tfrac{ 9}{10}),$ φ(5) = 4 fractions with denominator 5 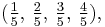$(\tfrac{ 1}{5},\,\tfrac{ 2}{5},\,\tfrac{ 3}{5},\,\tfrac{ 4}{5}),$ and so on. Since the same argument works for any number, not just 20, the formula is established.

Möbius inversion gives

$\varphi(n) =\sum_{d\mid n} d \cdot \mu\left(\frac{n}{d} \right) =n\sum_{d\mid n} \frac{\mu (d)}{d} ,$

where μ is the Möbius function.

This formula may also be derived from the product formula by mutiplying out 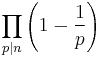$\prod_{p\mid n} \left(1-\frac{1}{p}\right)$ to get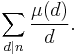 $\sum_{d\mid n} \frac{\mu (d)}{d}.$

Some values of the function

The first 99 values (sequence A000010 in OEIS) are shown in the table and graph below:

$\varphi(n)$	+0	+1	+2	+3	+4	+5	+6	+7	+8	+9
0+		1	1	2	2	4	2	6	4	6
10+	4	10	4	12	6	8	8	16	6	18
20+	8	12	10	22	8	20	12	18	12	28
30+	8	30	16	20	16	24	12	36	18	24
40+	16	40	12	42	20	24	22	46	16	42
50+	20	32	24	52	18	40	24	36	28	58
60+	16	60	30	36	32	48	20	66	32	44
70+	24	70	24	72	36	40	36	60	24	78
80+	32	54	40	82	24	64	42	56	40	88
90+	24	72	44	60	46	72	32	96	42	60

The top line, y = n − 1, is a true upper bound. It is attained whenever n is prime.
The lower line, y ≈ 0.267n which connects the points for n = 30, 60, and 90 is misleading. If the plot were continued, there would be points below it.
(Examples: for n = 210 = 7×30, φ(n) ≈ 0.229 n; for n = 2310 = 11×210 φ(n) ≈ 0.208 n; and for n = 30030 = 13×2310 φ(n) ≈ 0.192 n.)
In fact, there is no lower bound straight line; no matter how gentle the slope of a line (through the origin) is, there will eventually be points of the plot below the line.

Euler's theorem

Main article: Euler's theorem

This states that if a and n are relatively prime then

$a^{\varphi(n)} \equiv 1\mod n.\,$

This follows from Lagrange's theorem and the fact that φ(n) is the order of the multiplicative group of integers modulo n.

Other formulae involving φ

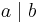$a\mid b$ implies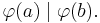 $\varphi(a)\mid\varphi(b).$

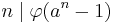$n \mid \varphi(a^n-1)$ (a, n > 1)

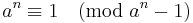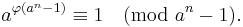
Proof: $a^n\equiv 1 \pmod {a^n-1}$ and $a^{\varphi(a^n - 1)} \equiv 1 \pmod{a^n-1}.$

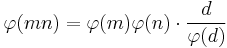$\varphi(mn) = \varphi(m)\varphi(n)\cdot\frac{d}{\varphi(d)}$ where d = gcd(m, n). Note the special cases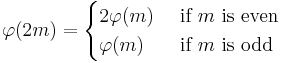
$\varphi(2m) = \begin{cases} 2\varphi(m) &\text{ if } m \text{ is even} \\ \varphi(m) &\text{ if } m \text{ is odd} \end{cases}$

and

$\;\varphi\left(n^m\right) = n^{m-1}\varphi(n).$

$\varphi(\mathrm{lcm}(m,n))\cdot\varphi(\mathrm{gcd}(m,n)) = \varphi(m)\cdot\varphi(n).$

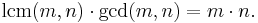Compare this to the formula $\mathrm{lcm}(m,n)\cdot \mathrm{gcd}(m,n) = m \cdot n.$ (See lcm).

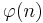$\varphi(n)\;$ is even for 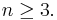$n \geq 3.$ Moreover, if n has r distinct odd prime factors,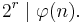 $2^r \mid \varphi(n).$

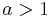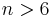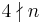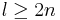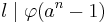For any $a > 1$ and $n > 6$ such that $4 \nmid n$ there exists an $l \geq 2n$ such that $l \mid \varphi(a^n-1)$ .

$\sum_{d \mid n} \frac{\mu^2(d)}{\varphi(d)} = \frac{n}{\varphi(n)}$ ^[11]

$\sum_{1\le k\le n \atop (k,n)=1}\!\!k = \frac{1}{2}n\varphi(n)\text{ for }n>1$

$\sum_{k=1}^n\varphi(k) = \frac{1}{2}\left(1%2B \sum_{k=1}^n \mu(k)\left\lfloor\frac{n}{k}\right\rfloor^2\right)$

$\sum_{k=1}^n\frac{\varphi(k)}{k} = \sum_{k=1}^n\frac{\mu(k)}{k}\left\lfloor\frac{n}{k}\right\rfloor$

$\sum_{k=1}^n\frac{k}{\varphi(k)} = \mathcal{O}(n).$ ^[12]

$\sum_{k=1}^n\frac{1}{\varphi(k)} = \mathcal{O}(\log(n))$

$\sum_{1\le k\le n \atop (k,m)=1} 1 = n \frac {\varphi(m)}{m} %2B \mathcal{O} \left ( 2^{\omega(m)} \right ),$

where m > 1 is a positive integer and ω(m) is the number of distinct prime factors of m. (a, b) is a standard abbreviation for gcd(a, b).^[13]

Formulae involving the golden ratio

Schneider^[14] found a pair of identities connecting the golden ratio and the natural log, φ and μ functions. In this section 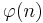$\varphi(n)\;$ is the totient function, and 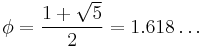$\phi = \frac{1%2B\sqrt{5}}{2}= 1.618\dots$ is the golden ratio.

They are:

$\phi=-\sum_{k=1}^\infty\frac{\varphi(k)}{k}\log\left(1-\frac{1}{\phi^k}\right)$

and

$\frac{1}{\phi}=-\sum_{k=1}^\infty\frac{\mu(k)}{k}\log\left(1-\frac{1}{\phi^k}\right).$

Subtracting them gives

$\sum_{k=1}^\infty\frac{\mu(k)-\varphi(k)}{k}\log\left(1-\frac{1}{\phi^k}\right)=1.$

The proof is based on the formulae

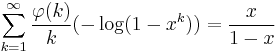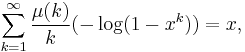$\sum_{k=1}^\infty\frac{\varphi(k)}{k}(-\log(1-x^k))=\frac{x}{1-x}$ and $\sum_{k=1}^\infty\frac{\mu(k)}{k}(-\log(1-x^k))=x,$ valid for 0 < x < 1.

Generating functions

The Dirichlet series for φ(n) may be written in terms of the Riemann zeta function as:^[15]

$\sum_{n=1}^\infty \frac{\varphi(n)}{n^s}=\frac{\zeta(s-1)}{\zeta(s)}.$

The Lambert series generating function is^[16]

$\sum_{n=1}^{\infty} \frac{\varphi(n) q^n}{1-q^n}= \frac{q}{(1-q)^2}$

which converges for |q| < 1.

Both of these are proved by elementary series manipulations and the formulae for φ(n).

Growth of the function

In the words of Hardy & Wright, φ(n) is "always ‘nearly n’."^[17]

First^[18]

$\lim\sup \frac{\varphi(n)}{n}= 1,$

but as n goes to infinity,^[19] for all δ > 0

$\frac{\varphi(n)}{n^{1-\delta}}\rightarrow\infty.$

These two formulae can be proved by using little more than the formulae for φ(n) and the divisor sum function σ(n).
In fact, during the proof of the second formula, the inequality

$\frac {6}{\pi^2} < \frac{\varphi(n) \sigma(n)}{n^2} < 1,$

true for n > 1, is proven.
We also have^[20]

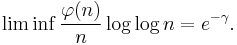$\lim\inf\frac{\varphi(n)}{n}\log\log n = e^{-\gamma}.$ Here γ is Euler's constant, γ = 0.577215665..., e^γ = 1.7810724..., e^−γ = 0.56145948... .

Proving this, however, requires the prime number theorem.^[21]^[22] Since log log (n) goes to infinity, this formula shows that

$\lim\inf\frac{\varphi(n)}{n}= 0.$

In fact, more is true.^[23]^[24]

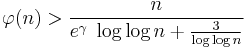$\varphi(n) > \frac {n} {e^\gamma\; \log \log n %2B \frac {3} {\log \log n}}$ for n > 2, and

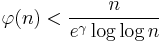$\varphi(n) < \frac {n} {e^{ \gamma}\log \log n}$ for infinitely many n.

Concerning the second inequality, Ribenboim says "The method of proof is interesting, in that the inequality is shown first under the assumption that the Riemann hypothesis is true, secondly under the contrary assumption."^[25]

For the average order we have^[26]

$\varphi(1)%2B\varphi(2)%2B\cdots%2B\varphi(n) = \frac{3n^2}{\pi^2}%2B\mathcal{O} (n\log n)$

The "Big O" stands for a quantity that is bounded by a constant times nlog n (which is negligible compared to n²).

This result can be used to prove^[27] that the probability of two randomly-chosen numbers being relatively prime is 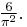$\tfrac{6}{\pi^2}.$

Ratio of consecutive values

In 1950 Somayajulu proved^[28]

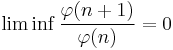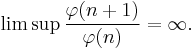
$\lim\inf \frac{\varphi(n%2B1)}{\varphi(n)}= 0$ and $\lim\sup \frac{\varphi(n%2B1)}{\varphi(n)}= \infty.$

In 1954 Schinzel and Sierpiński strengthened this, proving^[29] that the set

$\left\{\frac{\varphi(n%2B1)}{\varphi(n)},\;\;n = 1,2,\cdots\right\}$

is dense in the positive real numbers. They also proved^[30] that the set

$\left\{\frac{\varphi(n)}{n},\;\;n = 1,2,\cdots\right\}$

is dense in the interval (0, 1).

Ford's theorem

Ford (1999) proved that for every integer k ≥ 2 there is a number m for which the equation φ(x) = m has exactly k solutions; this result had previously been conjectured by Wacław Sierpiński. However, no such m is known for k = 1. Carmichael's totient function conjecture is the statement that there is no such m.

Applications

Cyclotomy

Main article: Constructible polygon

In the last section of the Disquisitiones^[31]^[32] Gauss proves^[33] that a regular n-gon can be constructed with ruler and compass if φ(n) is a power of 2. If n is a power of an odd prime number the formula for the totient says its totient can be a power of two only if a) n is a first power and b) n − 1 is a power of 2. The primes that are one more than a power of 2 are called Fermat primes, and only five are known: 3, 5, 17, 257, and 65537. Fermat and Gauss knew of these. Nobody has been able to prove that there are no more.

Thus, a regular n-gon has a ruler-and-compass construction if n is a product of distinct Fermat primes and any power of 2.
The first few such n are^[34] 2, 3, 4, 5, 6, 8, 10, 12, 15, 16, 17, 20, 24, 30, 32, 34, 40, ... . (sequence A003401 in OEIS)

The RSA cryptosystem

Main article: RSA (algorithm)

Setting up an RSA system involves choosing large prime numbers p and q, computing n = pq and k = φ(n), and finding two numbers e and d such that ed ≡ 1 (mod k). The numbers n and e (the "encryption key") are released to the public, and d (the "decryption key") is kept secure.

A message, represented by an integer m, where 0 < m < n, is encrypted by computing S = m^e (mod n).

It is decrypted by computing t = S^d (mod n). Euler's Theorem can be used to show that if 0 < t < n, then t = m.

The security of an RSA system would be compromised if the number n could be factored or if φ(n) could be computed without factoring n.

Unsolved problems

Lehmer's conjecture

If p is prime, then φ(p) = p − 1. In 1932 D. H. Lehmer asked if there are any composite numbers n such that φ(n) | n − 1. None is known.^[35]

In 1933 he proved that if any such n exists, it must be odd, square-free, and divisible by at least 7 primes (i.e. ω(n) ≥ 7). In 1980 Cohen and Hagis proved that n > 10²⁰ and that ω(n) ≥ 14. Further, in 1970 Lieuwens showed that if 3 | n then n > 5.5 × 10⁵⁷⁰ and ω(n) ≥ 213.

Carmichael's conjecture

Main article: Carmichael's totient function conjecture

This states that there is no number n with the property that for all other numbers m, m ≠ n, 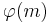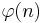$\varphi(m)$ ≠ $\varphi(n)$ . See Ford's theorem above.

As stated in the main article, if there is a single counterexample to this conjecture, there must be infinitely many counterexamples, and the smallest one has at least ten billion digits in base 10.

Notes

^ Sandifer, p. 203
^ Graham et al. p. 133 note 111
^ Sandifer, p. 203
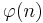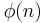^ Both $\varphi(n)\;$ and $\phi(n)\;$ are seen in the literature. These are two forms of the lower-case Greek letter phi
^ Gauss, DA art. 38
^ Graham et al., p. 133 note 347
^ Hardy & Wright, thm. 63, note to § 5.5
^ Gauss, DA, art 39
^ Gauss, DA art. 39, arts. 52-54
^ Graham et al. pp. 134-135
^ Dineva (in external refs), prop. 1
^ this and the next formula are straightforward deductions from the order-of-magnitude theorems in the "growth" section
^ Bordellès in the external links
^ All formulae in the section are from Schneider (in the external links)
^ Hardy & Wright, thm. 288
^ Hardy & Wright, thm. 309
^ Hardy & Wright, intro to § 18.4
^ Hardy & Wright, thm. 326
^ Hardy & Wright, thm. 327
^ Hardy & Wright, thm. 328
^ In fact Chebychev's theorem (Hardy & Wright, thm.7) is all that's needed
^ Hardy & Wright, thm. 436
^ Bach & Shallit, thm. 8.8.7
^ Ribenboim, p.320
^ Ribenboim, p. 320
^ Hardy & Wright, thm. 330
^ Hardy & Wright, thm. 332
^ Ribenboim, p.38
^ Ribenboim, p.38
^ Ribenboim, p.38
^ Gauss, DA. The 7th § is arts. 336-366
^ Gauss proved if n satisfies certain conditions then the n-gon can be constructed. In 1837 Pierre Wantzel proved the converse, if the n-gon is constructible, then n must satisfy Gauss's conditions
^ Gauss, DA, art 366
^ Gauss, DA, art. 366. This list is the last sentence in the Disquisitiones
^ All the information in this subsection is from Ribenboim, pp. 36-37.

References

The Disquisitiones Arithmeticae has been translated from Latin into English and German. The German edition includes all of Gauss' papers on number theory: all the proofs of quadratic reciprocity, the determination of the sign of the Gauss sum, the investigations into biquadratic reciprocity, and unpublished notes.

References to the Disquisitiones are of the form Gauss, DA, art. nnn.

Gauss, Carl Friedrich; Clarke, Arthur A. (translator into English) (1986), Disquisitiones Arithemeticae (Second, corrected edition), New York: Springer, ISBN 0387962549

Gauss, Carl Friedrich; Maser, H. (translator into German) (1965), Untersuchungen uber hohere Arithmetik (Disquisitiones Arithemeticae & other papers on number theory) (Second edition), New York: Chelsea, ISBN 0-8284-0191-8

Abramowitz, M.; Stegun, I. A. (1964), Handbook of Mathematical Functions, New York: Dover Publications, ISBN 0-486-61272-4 . See paragraph 24.3.2.

Bach, Eric; Shallit, Jeffrey (1966), Algorithmic Number Theory (Vol I: Efficient Algorithms), Cambridge: The MIT Press, ISBN 0-262-02045-5

Ford, K. (1999), "The number of solutions of φ(x) = m", Annals of Mathematics 150 (1): 283–311, doi:10.2307/121103, JSTOR 121103, MR 1715326 .

Graham, Ronald; Knuth, Donald; Patashnik, Oren (1994), Concrete Mathematics, Reading Ma: Addison-Wesley, ISBN 0-201-55802-5

Hardy, G. H.; Wright, E. M. (1980), An Introduction to the Theory of Numbers (Fifth edition), Oxford: Oxford University Press, ISBN 978-0198531715

Ribenboim, Paulo (1996), The New Book of Prime Number Records, New York: Springer, ISBN 0-387-94457-5

Sandifer, Charles (2007), The early mathematics of Leonhard Euler, MAA, ISBN 0-883-85559-3

Schramm, Wolfgang (2008), "The Fourier transform of functions of the greatest common divisor", Electronic Journal of Combinatorial Number Theory A50 (8(1)), http://www.integers-ejcnt.org/vol8.html .

External links

Kirby Urner, Computing totient function in Python and scheme, (2003)

Euler's totient function calculator in JavaScript - up to 20 digits

Bordellès, Olivier, Numbers prime to q in $[1, n]$

Dineva, Rosica, The Euler Totient, the Möbius, and the Divisor Functions

Miyata, Daisuke & Yamashita, Michinori, Derived logarithmic function of Euler's function

Plytage, Loomis, Polhill Summing Up The Euler Phi Function

Schneider, Robert P. A Golden Pair of Identities in the Theory of Numbers

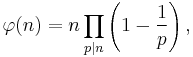
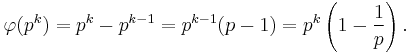
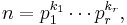
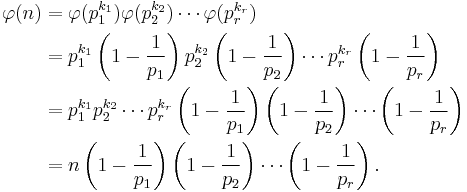
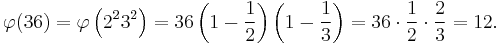
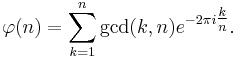
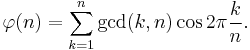
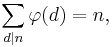
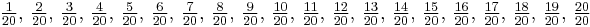
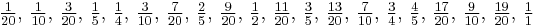
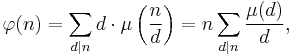
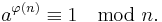
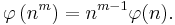
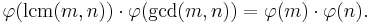
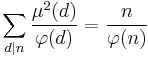
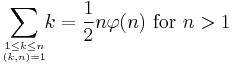
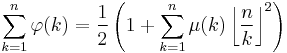
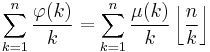
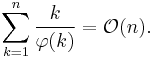
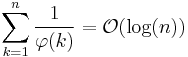
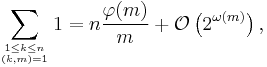
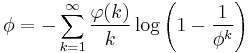
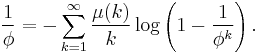
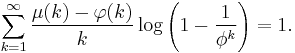
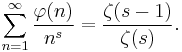
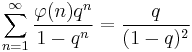
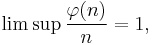
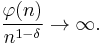
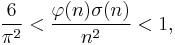
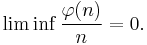
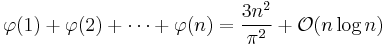
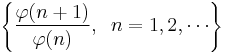
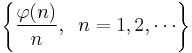
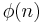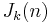Totient function

Euler's totient function $\phi(n)$ · Jordan's totient function $J_k(n)$ · Nontotient · Noncototient · Highly totient number · Sparsely totient number · Highly cototient number

Euler's totient function

Contents

History, terminology, and notation

Computing Euler's function

Euler's product formula

φ(n) is multiplicative

φ(p^k) = p^k − p^{k − 1} = p^{k − 1}(p − 1)

Example

Fourier transform

Divisor sum

Some values of the function

Euler's theorem

Other formulae involving φ

Formulae involving the golden ratio

Generating functions

Growth of the function

Ratio of consecutive values

Ford's theorem

Applications

Cyclotomy

The RSA cryptosystem

Unsolved problems

Lehmer's conjecture

Carmichael's conjecture

See also

Notes

References

External links

$\varphi(n)$	+0	+1	+2	+3	+4	+5	+6	+7	+8	+9
0+		1	1	2	2	4	2	6	4	6
10+	4	10	4	12	6	8	8	16	6	18
20+	8	12	10	22	8	20	12	18	12	28
30+	8	30	16	20	16	24	12	36	18	24
40+	16	40	12	42	20	24	22	46	16	42
50+	20	32	24	52	18	40	24	36	28	58
60+	16	60	30	36	32	48	20	66	32	44
70+	24	70	24	72	36	40	36	60	24	78
80+	32	54	40	82	24	64	42	56	40	88
90+	24	72	44	60	46	72	32	96	42	60

$\varphi(n)$	+0	+1	+2	+3	+4	+5	+6	+7	+8	+9
0+		1	1	2	2	4	2	6	4	6
10+	4	10	4	12	6	8	8	16	6	18
20+	8	12	10	22	8	20	12	18	12	28
30+	8	30	16	20	16	24	12	36	18	24
40+	16	40	12	42	20	24	22	46	16	42
50+	20	32	24	52	18	40	24	36	28	58
60+	16	60	30	36	32	48	20	66	32	44
70+	24	70	24	72	36	40	36	60	24	78
80+	32	54	40	82	24	64	42	56	40	88
90+	24	72	44	60	46	72	32	96	42	60

Euler's totient function

Contents

History, terminology, and notation

Computing Euler's function

Euler's product formula

φ(n) is multiplicative

φ(pk) = pk − pk − 1 = pk − 1(p − 1)

Example

Fourier transform

Divisor sum

Some values of the function

Euler's theorem

Other formulae involving φ

Formulae involving the golden ratio

Generating functions

Growth of the function

Ratio of consecutive values

Ford's theorem

Applications

Cyclotomy

The RSA cryptosystem

Unsolved problems

Lehmer's conjecture

Carmichael's conjecture

See also

Notes

References

External links

φ(p^k) = p^k − p^{k − 1} = p^{k − 1}(p − 1)

$\varphi(n)$	+0	+1	+2	+3	+4	+5	+6	+7	+8	+9
0+		1	1	2	2	4	2	6	4	6
10+	4	10	4	12	6	8	8	16	6	18
20+	8	12	10	22	8	20	12	18	12	28
30+	8	30	16	20	16	24	12	36	18	24
40+	16	40	12	42	20	24	22	46	16	42
50+	20	32	24	52	18	40	24	36	28	58
60+	16	60	30	36	32	48	20	66	32	44
70+	24	70	24	72	36	40	36	60	24	78
80+	32	54	40	82	24	64	42	56	40	88
90+	24	72	44	60	46	72	32	96	42	60